2 related rates
2 optimization
1 differentiability
5 limits
1 continuity
2 applications
1 antiderivative
5 derivatives
1 max & min
Category Archives: Uncategorized
Calculus Review Solutions
2. a. b.
3.
4. left and right hand limits don’t agree
5. 0
6. left and right hand limits don’t agree
7.
8. 54
9.
10.
11.
12.
13.
14.
15. -1
16.
17.
18. 
80 feet
19.
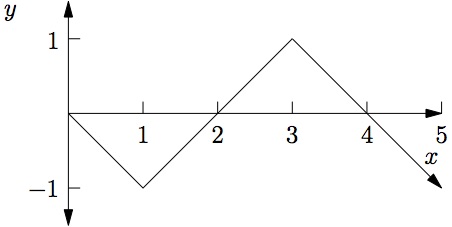
20. 
Calculus Practice Final
Trigonometry Classwork Solutions
,
Trigonometry Classwork 5-23-17
In 1-9, solve each equation for such that
.
- Solve for
such that
and round to the nearest thousandth:
Calculus Homework #12 Due 5-25
Calculate the following definite integrals
1.
2.
3.
4.
Trigonometry Homework #12 due 5-25
Solve each equation for
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Calculus Homework #11 due 5-18

Given the graph of above, calculate the following definite integrals.
Trigonometry Homework #11 due 5-18
Prove each identity.
Trigonometry Classwork 5-9
- What is the equation of this function?

2. What is the equation of this function?

3. Graph
4. Graph
5. Graph
You must be logged in to post a comment.