Monthly Archives: February 2017

Standard

Posted by

Posted on

February 18, 2017

Posted under

Uncategorized

Comments

Leave a comment

Calculus reading for 2-27

If you look at the course calendar you will see that you need to read section 2.4 for Monday the 27th. I realize, however, that many of you still don’t have textbooks. Since I forgot to scan the section yesterday, I’ll give you an option. You can read section 2.4, or you can watch this video instead.

Standard

Posted by

Posted on

February 10, 2017

Posted under

Uncategorized

Comments

Leave a comment

Calculus homework #2 due 2-16

  1. Does \lim_{x\rightarrow 1}\cot(\pi x) exist? Explain your answer.
  2. Consider the graph of f(x)

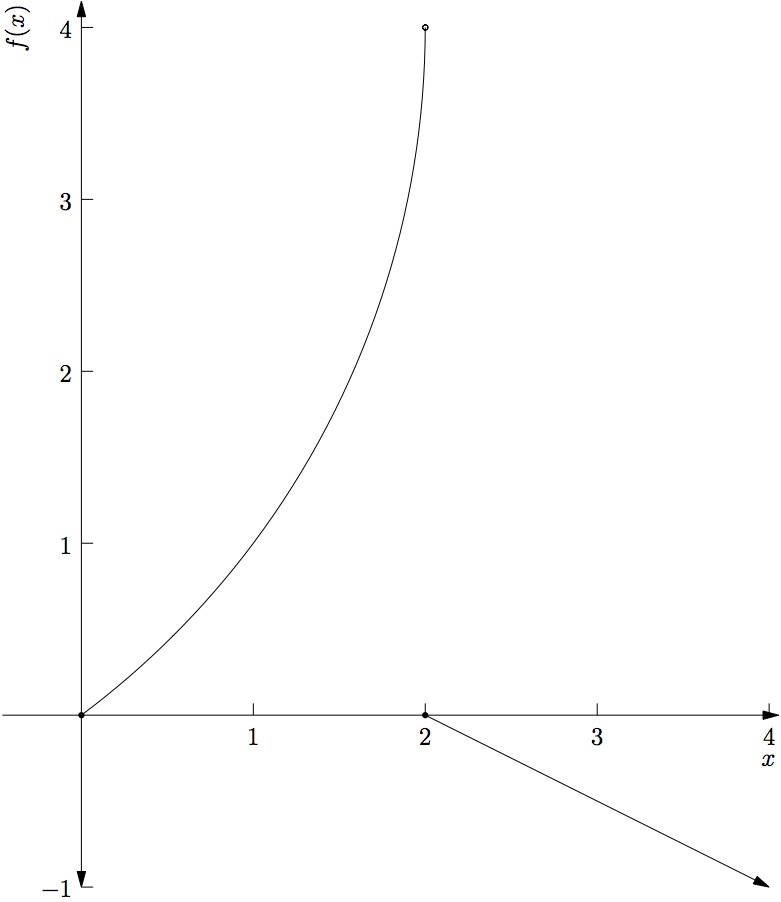
homework1

State the value of each quantity, if it exists. If it does not exist, explain why.

\lim_{x\rightarrow 0}f(x)    \lim_{x\rightarrow 0^{+}}f(x)    \lim_{x\rightarrow 2^{-}}f(x)    f(2)    \lim_{x\rightarrow 2}f(x)

3. Sketch the graph of an example of a function f(x) such that \lim_{x\rightarrow 2}f(x)=3, \lim_{x\rightarrow -2}f(x)=0, and f(2)=f(-2)=1.

4. Sketch the graph of an example of a function f(x) such that \lim_{x\rightarrow -1^{-}}f(x)=4, \lim_{x\rightarrow 1^{-}}f(x)=2, and f(x) is even.

Standard

Posted by

Posted on

February 10, 2017

Posted under

Uncategorized

Comments

Leave a comment

Trigonometry Homework #2 due 2-16

  1. Find the unique polynomial P(x) which satisfies the below list of conditions and write it in the form P(x)=a_nx^n+\cdots+a_1x+a_0.
    • the degree is as small as possible
    • the coefficients are real
    • P(4)=0
    • P\left(\frac{-i}{3}\right)=0
    • P(0)=1
  2. Sketch a graph of f(x)=x^3-3x^2+4x-12.
  3. Re-write x^5+x^4+x^3+x^2-12x-12 as a product of linear factors.
  4. Given f(x)=ax^3-bx^2+3x+4 and the graph of f(x) below, find a and bucogydvo7k
  5. Write the algebraic definition of the polynomial function graphed below.6pd7zqmrch
Standard

Posted by

Posted on

February 3, 2017

Posted under

Uncategorized

Comments

Leave a comment

Trigonometry Homework #1 due 2-9

In 1-6, divide the polynomials.

1. \frac{9u^4+6u^3+4u+4}{3u^2+2u+2}

2. \frac{x^3+a^3+4a^2x+4ax^2}{x+2a}

3. \frac{6t^4+ct^3-c^3t+c^4}{2t^2+ct+c^2}

4. \frac{x^6+x^5+x^3+x+1}{x^4-x^2+1}

5. \frac{x^4+a^4}{x^2+a^2}

6. \frac{x^6-a^6}{x^2+ax+a^2}

7. When x^3-7x+4 is divided by the polynomial D(x), the quotient is x^2-3x+2 and the remainder is -2. Find D(x).

8. Find k so that when x^3+kx^2-kx+1 is divided by x-2, the remainder is 0.

9. Find k so that when x^3+kx^2+k^2x+14 is divided by x+2, the remainder is 0.

10. When 3x^2-5x+c is divided by x+k, the quotient is 3x+1 and the remainder is 3. Find c and k.